2157. Sum
Roman’s parents
gave him an undirected, connected, weighted graph with n vertices and n – 1 edges. Roman wants to find the
total length of all paths between every pair of vertices in the graph. The
length of a path is defined as the sum of the weights of the edges it includes.
Since the path from vertex u to vertex v is the same as the path
from v to u, Roman treats them as a single path and does not
distinguish between them.
Input. The first line
contains an integer n (2 ≤ n ≤ 105) – the
number of vertices in the graph.
Each of the next n – 1 lines describes an edge and
contains three integers: the numbers of the two vertices connected by the edge
(vertices are numbered from 1 to n), and the weight of the edge.
Output. Print the total
length of all distinct paths between all pairs of vertices, modulo 109.
|
Sample
input 1 |
Sample
output 1 |
|
3 1 2 1 1 3 3 |
8 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
6 1 2 5 1 3 1 2 4 2 2 5 4 2 6 3 |
90 |
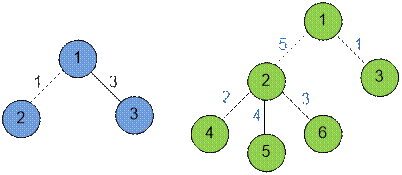
In the first example, all the paths in the tree are as
follows: 1 – 2, 1 – 3, and 2 – 1 – 3. Their lengths are 1, 3, and 4
respectively, and the sum of these lengths is 1 + 3 + 4 = 8.
SOLUTION
graphs, depth
first search, tree
Algorithm analysis
Perform a depth-first search starting from an arbitrary vertex of the
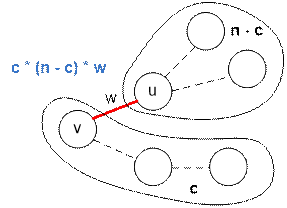
tree. Consider an edge (u, v) with weight w. Let the number of
vertices in the subtree rooted at v be c. Then, there are c
vertices on one side of the edge and n – c vertices on the other side. The edge (u, v) is included in c * (n – c) distinct paths between pairs of vertices. Therefore, its
contribution to the total length of all paths is c * (n – c) * w. We just need to iterate over all
edges using depth-first search and sum up their contributions to the overall
path length.
Example
The graphs given in the examples have the following
structure:
Consider the contribution of the edges to the total length of all paths in the
first example.
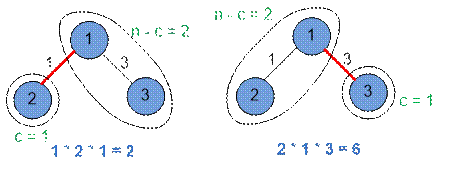
The edge (1, 2) with weight 1 belongs to two paths:
·
1 – 2;
·
2 – 1 – 3;
Its contribution to the total sum is 1 * 2 * 1 = 2.
The edge (1, 3) with weight 3 belongs to two
paths:
·
1 – 3;
·
2 – 1 – 3;
Its contribution to the total sum is 2 * 1 * 3 = 6.
The total length of all paths is 2 + 6 = 8.
In the second example, let us consider the contribution of the edge (1, 2)
with weight 5 to the total length of all paths.
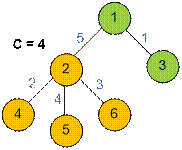
The number of vertices in the subtree rooted at vertex 2 is c = 4 (including vertex
2 itself). Then, on the other side of the edge (1, 2) there are n – c = 6 – 4 = 2 vertices. Therefore, the number of distinct
paths passing through the edge (1, 2) is c * (n – c)
= 4 * 2 = 8.
Indeed, these are all pairs of vertices where one lies in the subtree of
vertex 2, and the other lies outside of it:
1 – 2, 1 – 2 – 4, 1 – 2 – 5, 1 – 2 – 6,
3 – 1 – 2, 3 – 1 – 2 – 4, 3 – 1 – 2 – 5,
3 – 1 – 2 – 6
The contribution
of the edge (1, 2) with weight 5 to the total length of all
paths is
c * (n – c) * w = 4 * 2 * 5 = 40
Algorithm implementation
Declare the value of the
modulo as MOD.
#define MOD 1000000000
The input weighted graph
is stored in an adjacency list g.
vector<vector<pair<int,int> > > g;
The function dfs performs a depth-first search starting from
vertex v and returns the number of vertices in the subtree rooted at v
(including v itself). The number of such vertices is counted in the
variable cnt. Initially, set cnt = 1 since the subtree already
includes vertex v.
int dfs(int
v, int p = -1)
{
int cnt = 1;
for (auto edge : g[v])
{
int to = edge.first;
int w = edge.second;
Consider the edge (v, to) with weight w. Let c be the number of
vertices in the subtree rooted at vertex to. Then, one side of the edge
contains c vertices, and the other side contains n – c vertices. The edge (v, to) is included in c * (n – c) different paths between pairs of vertices. Thus, the
contribution of the edge (v, to) to the total length of all paths is
c * (n – c) * w
if (to != p)
{
int c = dfs(to, v);
res = (res + 1LL
* c * (n - c) * w) % MOD;
cnt += c;
}
}
return cnt;
}
The main part of the program. Read the input weighted graph into the adjacency
list g.
scanf("%d", &n);
g.resize(n + 1);
for(i = 1; i < n; i++)
{
scanf("%d %d %d", &u, &v, &d);
g[u].push_back({v, d});
g[v].push_back({u, d});
}
Start a depth-first search from vertex 1. The vertices of the graph are numbered
from 1 to n.
dfs(1);
Print the answer.
printf("%lld\n",res);
Java implementation
import java.util.*;
import java.io.*;
class Edge
{
int to;
int weight;
public Edge(int to, int weight)
{
this.to = to;
this.weight = weight;
}
}
public class Main
{
static int MOD = 1000000000;
static
ArrayList<Edge>[] g;
static int n, m;
static long res;
static int dfs(int v, int p)
{
int cnt = 1;
for(Edge edge : g[v])
{
int to = edge.to;
int w = edge.weight;
if (to != p)
{
int c = dfs(to, v);
res = (res + 1L * c * (n - c) * w) % MOD;
cnt += c;
}
}
return cnt;
}
public static void main(String[] args)
{
FastScanner con = new FastScanner(System.in);
n = con.nextInt();
g = new ArrayList[n+1]; // unchecked
for (int i = 0; i <= n; i++)
g[i] = new ArrayList<Edge>();
for (int i = 1; i < n; i++)
{
int u = con.nextInt();
int v = con.nextInt();
int d = con.nextInt();
g[u].add(new Edge(v,d));
g[v].add(new Edge(u,d));
}
dfs(1,-1);
System.out.println(res);
}
}
class FastScanner
{
BufferedReader br;
StringTokenizer st;
public FastScanner(InputStream inputStream)
{
br = new BufferedReader(new InputStreamReader(inputStream));
st = new StringTokenizer("");
}
public String next()
{
while (!st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch (Exception e)
{
return null;
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
}
Python implementation
Declare the value of the
modulo as MOD.
MOD = 1000000000
The function dfs performs a depth-first search starting from
vertex v and returns the number of vertices in the subtree rooted at v
(including v itself). The number of such vertices is counted in the
variable cnt. Initially, set cnt = 1 since the subtree already
includes vertex v.
def dfs(v, p = -1):
global res
cnt = 1
for to, w in g[v]:
Consider the edge (v, to) with weight w. Let c be the number of
vertices in the subtree rooted at vertex to. Then, one side of the edge
contains c vertices, and the other side contains n – c vertices. The edge (v, to) is included in c * (n – c) different paths between pairs of vertices. Thus, the
contribution of the edge (v, to) to the total length of all paths is
c * (n – c) * w
if to != p:
c = dfs(to, v)
res = (res + c * (n - c) * w) % MOD
cnt += c
return cnt
The main part of the program. Read the input data.
n = int(input())
g = [[] for _ in
range(n + 1)]
res = 0
for _ in range(n - 1):
u, v, d = map(int, input().split())
g[u].append((v, d))
g[v].append((u, d))
Start a depth-first search from vertex 1. The vertices of the graph are numbered
from 1 to n.
dfs(1)
Print the answer.
print(res)